ಬೆಳಕಿನ ಕೋಲು ಮೂಡುವುದಾದರೂ ಹೇಗೆ?

ಗೆಲಿಲಿಯೋ ಹೇಳಿದ ಅನಂತದ ಮಹಾ ಪುಸ್ತಕವನ್ನು ಅರ್ಥಮಾಡಿಕೊಳ್ಳುವಲ್ಲಿ, ಈ ವಿಧಾನ ಅತ್ಯಂತ ಪರಿಣಾಮಕಾರಿಯಾಗಿ ಕೆಲಸಮಾಡಿದೆ. ಇದರಿಂದಾಗಿ, ಹಿಂದೊಮ್ಮೆ ಪ್ರಕೃತಿಯ ಗುಹ್ಯಾತಿಗುಹ್ಯವೆನಿಸಿದ್ದ ಎಷ್ಟೋ ರಹಸ್ಯಗಳು ಇಂದು ರಹಸ್ಯಗಳಾಗಿ ಉಳಿದಿಲ್ಲ. “ಚಂದಿರನೇತಕೆ ಓಡುವನಮ್ಮ” ಎನ್ನುವ ಬದಲು, ಚಂದ್ರನ ಮೇಲೆಯೇ ಕಾಲಿಟ್ಟು ಬಂದಾಗಿದೆ. ವಿಜ್ಞಾನ, ಅದರಲ್ಲೂ ಭೌತ ಶಾಸ್ತ್ರ, ಗೆಲಿಲಿಯೋ-ನ್ಯೂಟನ್ ನಂತರದ ಶತಮಾನಗಳಲ್ಲಿ, ಗಣಿತದ ಕೈಹಿಡಿದೇ ನಡೆದಿದೆ.
ಶೇಷಾದ್ರಿ ಗಂಜೂರು ಬರೆಯುವ ಅಂಕಣ

 

ಕ್ರಿ.ಶ.1623ರಲ್ಲಿ ಗೆಲಿಲಿಯೋನ ಒಂದು ಪುಸ್ತಕ ಪ್ರಕಟವಾಯಿತು. ಅದರ ಹೆಸರು ‘ಇಲ್ ಸಜಿಯಟೋರೆ”. (ಅದರ ಸಂಕ್ಷಿಪ್ತ ಇಂಗ್ಲೀಷ್ ಅನುವಾದ ಇಲ್ಲಿದೆ: https://web.stanford.edu/~jsabol/certainty/readings/Galileo-Assayer.pdf) ಅದು ಒಂದು ಸಣ್ಣ ಪುಸ್ತಕ; ಅದರಲ್ಲಿನ ಚಿತ್ರಗಳೂ ಸೇರಿ, ಅದರ ಗಾತ್ರ ಕೇವಲ ಸುಮಾರು ೧೨೦ ಪುಟಗಳಷ್ಟೇ. ಆ ಪುಸ್ತಕ ಸಣ್ಣದಾದರೂ, ವಿಜ್ಞಾನದ ಚರಿತ್ರೆಯಲ್ಲಿ ಅದರ ಮಹತ್ವ ಮಾತ್ರ ಸಣ್ಣದಲ್ಲ. ಆ ಪುಸ್ತಕದಲ್ಲಿ, ಗೆಲಿಲಿಯೋ, ವಸ್ತುವೊಂದರ ವಾಸನೆ ಮತ್ತು ರುಚಿಗಳು ನಮ್ಮ ಅನುಭವಕ್ಕೆ ಬರುವುದು ಆ ವಸ್ತುಗಳಲ್ಲಿರುವ ಅತ್ಯಂತ ಸಣ್ಣ ಕಣಗಳಿಂದ ಎಂದೆನ್ನುತ್ತಾನೆ. ಇದು ನಮಗೆ ಇಂದು ಅತ್ಯಂತ ಸಾಮಾನ್ಯವೆನ್ನಿಸಬಹುದು, ಆದರೆ, ನಾಲ್ಕುನೂರು ವರ್ಷಗಳ ಹಿಂದೆ, ಇದೊಂದು ಹೊಸ ಹೊಳಹು.

 

ಗೆಲಿಲಿಯೋನ ಆ ಪುಸ್ತಕ ಮುಖ್ಯವಾಗುವುದು, ವಾಸನೆ ಮತ್ತು ರುಚಿಗಳ ಕುರಿತಾದ ಅವನ ಆಲೋಚನೆಗಳಿಗಲ್ಲ. ಬದಲಿಗೆ, ಸೃಷ್ಟಿಯ ಅನಂತವನ್ನು ತೆರೆದ ಪುಸ್ತಕಕ್ಕೆ ಹೋಲಿಸುತ್ತಾ ಅವನೆಂದ ಈ ಮಾತುಗಳಿಗೆ: “ಈ ಮಹಾ ಪುಸ್ತಕ ನಮಗೆ ಸದಾ ತೆರದೇ ಇದೆ. ಆದರೆ, ಅದನ್ನು ಅರ್ಥ ಮಾಡಿಕೊಳ್ಳಲು ನಾವು ಅದರ ಭಾಷೆಯನ್ನು ಮೊದಲು ಕಲಿಯಬೇಕು. ಗಣಿತ ಅದರ ಭಾಷೆ. ಗಣಿತವನ್ನು ತಿಳಿಯದೆ ಈ ಪುಸ್ತಕದ ಒಂದೇ ಒಂದು ಪದವನ್ನೂ ಅರ್ಥಮಾಡಿಕೊಳ್ಳುವುದು ಅಸಾಧ್ಯ. ಗಣಿತವಿಲ್ಲದಿದ್ದರೆ, ನಾವು ಕಗ್ಗತ್ತಲ ಚಕ್ರವ್ಯೂಹದಲ್ಲಿ ತಡಕಾಡುತ್ತಲೇ ಇರಬೇಕು.”

ಸೃಷ್ಟಿಯ ಅನಂತದ ಈ “ಮಹಾ ಪುಸ್ತಕ” ಗೆಲಿಲಿಯೋ ಹೇಳಿದಂತೆ ಸದಾ ತೆರದೇ ಇದೆ. ಅದನ್ನು ಓದುವ ಪ್ರಯತ್ನಗಳೂ ಮಾನವ ಇತಿಹಾಸದ ಉಗಮದಿಂದಲೂ ನಡೆದೇ ಇದೆ. ಅದಕ್ಕೆ ನಾವು ನೀಡಿರುವ ಹೆಸರು, “ವಿಜ್ಞಾನ”. ಆದರೆ, ಗೆಲಿಲಿಯೋ, ತನ್ನ ಆಲೋಚನೆಗಳ ಮೂಲಕ ಆ “ಮಹಾ ಪುಸ್ತಕ”ವನ್ನು ಓದಲು ಹೊಸದೊಂದು ವಿಧಾನವನ್ನು ತೋರಿಸಿಕೊಟ್ಟ; “ವಿಜ್ಞಾನ” ಎನ್ನುವುದು ಗಣಿತದ ಅಡಿಪಾಯದ ಮೇಲೆ ನಿಂತಿರುವುದನ್ನು ಅತ್ಯಂತ ಸುಸ್ಪಷ್ಟವಾಗಿ ಹೇಳಿದ.

ಗಣಿತ, ಆಧುನಿಕ ವಿಜ್ಞಾನಕ್ಕೂ ಹಿಂದಿನದು. “ದೊಡ್ಡದು/ಚಿಕ್ಕದು”, “ಹೆಚ್ಚು/ಕಡಿಮೆ” ಇಂತಹ ತುಲನೆಯನ್ನು ಹಲವಾರು ಪ್ರಾಣಿಗಳೂ ಮಾಡಬಲ್ಲವು. ಹೀಗಾಗಿ ಗಣಿತ ಎನ್ನುವುದು ಕೆಲ ಮಟ್ಟಿಗೆ ಹುಟ್ಟಿನಿಂದಲೇ ಬರುವಂತಹ ಅರಿವು. ಗಣಿತವನ್ನು, ಗೆಲಿಲಿಯೋ ಹುಟ್ಟುವ ಸಹಸ್ರಾರು ವರ್ಷಗಳ ಮುನ್ನವೇ ಭಾರತೀಯರೂ ಸೇರಿದಂತೆ ವಿಶ್ವದ ಎಲ್ಲಾ ಪುರಾತನ ಸಂಸ್ಕೃತಿಗಳವರು ಖಗೋಳ ಶಾಸ್ತ್ರಕ್ಕೆ, ಭವಿಷ್ಯ “ಶಾಸ್ತ್ರ”ಕ್ಕೆ ಬಳಸಿಕೊಂಡಿದ್ದಾರೆ. ಆದರೆ, ಗೆಲಿಲಿಯೋ “ಗಣಿತ” ಕೇವಲ ವಿಜ್ಞಾನದ “ಸಲಕರಣೆ”ಯಲ್ಲ ಅದರ “ಭಾಷೆ” ಎನ್ನುವವರೆಗೂ ಯಾರೂ ವಿಜ್ಞಾನ-ಗಣಿತಗಳ ಸಂಬಂಧದ ಕುರಿತು ಅಷ್ಟೊಂದು ಆಳವಾಗಿ ಆಲೋಚನೆ ಮಾಡಿರಲಿಲ್ಲ.

ಗೆಲಿಲಿಯೋ ನಂತರದಲ್ಲಿ, ವಿಜ್ಞಾನವನ್ನು ಗಣಿತದ ಬುನಾದಿಯ ಮೇಲೆ ಮತ್ತಷ್ಟು ಭದ್ರವಾಗಿಸಿದವನು ಐಸಾಕ್ ನ್ಯೂಟನ್. ಅವನು ತನ್ನ ವಿಜ್ಞಾನವನ್ನು ಮತ್ತಷ್ಟು ಗಟ್ಟಿಗೊಳಿಸಲು, ಗಣಿತದ ಹೊಸದೊಂದು ವಿಧಾನವೇ ಆದ “ಕ್ಯಾಲ್ಕುಲಸ್” ಸೃಷ್ಟಿಸಿದವನು.

ಗೆಲಿಲಿಯೋ-ನ್ಯೂಟನ್ ನಂತರದ ವರ್ಷಗಳಲ್ಲಿ, ವಿಜ್ಞಾನಕ್ಕೆ ಅವರಿಬ್ಬರು ಹಾಕಿಕೊಟ್ಟ ಒಂದು ಮಾದರಿ ನಿರ್ಮಿತವಾಗಿದೆ. ಆ ಮಾದರಿಯನ್ನು ನಾವು ಸ್ಥೂಲವಾಗಿ ಹೀಗೆ ಹೇಳಬಹುದು:

೧. ಪ್ರಕೃತಿಯಲ್ಲಿ ನಡೆಯುವ ಅಥವಾ ಪ್ರಯೋಗಗಳ ಆಗುಹೋಗುಗಳನ್ನು ಅತ್ಯಂತ ಎಚ್ಚರಿಕೆಯಿಂದ ಗಮನಿಸಿ, ಅವನ್ನು ಗಣಿತದ ಥಿಯರಿಯ ರೂಪದಲ್ಲಿ ವ್ಯಕ್ತಪಡಿಸುವುದು.
೨. ಆ ಥಿಯರಿಯನ್ನು ಬಳಸಿ “ಮುಂದೆ ಹೀಗಾಗುತ್ತದೆ” ಎಂದು ಭವಿಷ್ಯ (predictions) ಹೇಳುವುದು.
೩. ಆ ಭವಿಷ್ಯದ ಸತ್ಯಾಸತ್ಯತೆಗಳನ್ನು ಮತ್ತಷ್ಟು ಪ್ರಯೋಗ/ಅವಲೋಕನಗಳ ಮೂಲಕ ಪರಿಶೀಲಿಸುವುದು.

ಗೆಲಿಲಿಯೋ ಹೇಳಿದ ಅನಂತದ ಮಹಾ ಪುಸ್ತಕವನ್ನು ಅರ್ಥಮಾಡಿಕೊಳ್ಳುವಲ್ಲಿ, ಈ ವಿಧಾನ ಅತ್ಯಂತ ಪರಿಣಾಮಕಾರಿಯಾಗಿ ಕೆಲಸಮಾಡಿದೆ. ಇದರಿಂದಾಗಿ, ಹಿಂದೊಮ್ಮೆ ಪ್ರಕೃತಿಯ ಗುಹ್ಯಾತಿಗುಹ್ಯವೆನಿಸಿದ್ದ ಎಷ್ಟೋ ರಹಸ್ಯಗಳು ಇಂದು ರಹಸ್ಯಗಳಾಗಿ ಉಳಿದಿಲ್ಲ. “ಚಂದಿರನೇತಕೆ ಓಡುವನಮ್ಮ” ಎನ್ನುವ ಬದಲು, ಚಂದ್ರನ ಮೇಲೆಯೇ ಕಾಲಿಟ್ಟು ಬಂದಾಗಿದೆ. ವಿಜ್ಞಾನ, ಅದರಲ್ಲೂ ಭೌತ ಶಾಸ್ತ್ರ, ಗೆಲಿಲಿಯೋ-ನ್ಯೂಟನ್ ನಂತರದ ಶತಮಾನಗಳಲ್ಲಿ, ಗಣಿತದ ಕೈಹಿಡಿದೇ ನಡೆದಿದೆ. ಅವರೀರ್ವರ ನಂತರ ಬಂದ ದೆಕಾರ್ತ್, ಹಯ್ಗೆನ್ಸ್, ಲಪ್ಲಾಸ್, ಮುಂತಾದ ಮಹಾನ್ ವಿಜ್ಞಾನಿಗಳು, ಗಣಿತ ಶಾಸ್ತ್ರದಲ್ಲೂ ಹೆಸರು ಮಾಡಿರುವುದು ಕೇವಲ ಕಾಕತಾಳೀಯವೇನಲ್ಲ. ಅಥವಾ ಇದು ಕೇವಲ, ಶತಮಾನಗಳ ಹಿಂದಿನ ಯೂರೋಪಿಯನ್ ವಿಜ್ಞಾನಿಗಳಿಗೆ ಅನ್ವಯಿಸುವ ಮಾತಷ್ಟೇ ಅಲ್ಲ; ಭಾರತೀಯರೇ ಆದ, ಸಿ.ವಿ.ರಾಮನ್, ಎಸ್.ಚಂದ್ರಶೇಖರ್ ಸಹ ಗಣಿತದಲ್ಲಿ ನಿಪುಣರೇ. (ಕಳೆದ ಎರಡು ಶತಮಾನಗಳಲ್ಲಿ, ಗಣಿತ ಶಾಸ್ತ್ರ ತನ್ನದೇ ಆದ ವಿಶಿಷ್ಟತೆಯನ್ನು ಮೆರೆಯುತ್ತಿದೆ ಎಂಬುದೂ ನಿಜವಾದರೂ)

ಭೌತ ಶಾಸ್ತ್ರ – ಗಣಿತ ಶಾಸ್ತ್ರಗಳು ಕೈ-ಕೈ ಹಿಡಿದು ನಡೆಯುವ ಈ ಗೆಲಿಲಿಯೋ-ನ್ಯೂಟನ್ ಮಾದರಿಗೆ ಒಂದು ಅಪವಾದವೆಂದರೆ, ಅವನು ಮೈಕೇಲ್ ಫ್ಯಾರಡೆ. ತನ್ನ ಬಾಲ್ಯದಲ್ಲಿ ಕ್ರಮ ಶಿಕ್ಷಣ ಪಡೆಯಲು ಸಾಧ್ಯವಾಗದ್ದರಿಂದ ಅವನಿಗೆ, ತನ್ನ ವೈಜ್ಞಾನಿಕ ಕಲ್ಪನಾಶಕ್ತಿಗೆ ಬೇಕಿದ್ದ ಗಣಿತದ ನೈಪುಣ್ಯತೆ ಇರಲಿಲ್ಲ. ಅವನು, ತನ್ನ ಎಲೆಕ್ಟ್ರೋ-ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫೀಲ್ಡ್ ಸಿದ್ಧಾಂತವನ್ನು ಹೊರ ತಂದಿದ್ದು, ಗಣಿತದ ಥಿಯರಿಯ ಮೂಲಕವಲ್ಲ; ಅದು ಹೇಗೆ ಕಾಣಬಹುದೆಂದು ಊಹಿಸಿ ನಿರ್ಮಿಸಿದ ರೂಪಕಗಳ ಮೂಲಕ.

ಮೈಕೇಲ್ ಫ್ಯಾರಡೆ ತನ್ನ ಎಲೆಕ್ಟ್ರೋ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫೀಲ್ಡ್‌ ವಿಚಾರವನ್ನು ಪ್ರಕಟಿಸಿದ ಮೂವತ್ತು ವರ್ಷಗಳ ನಂತರ, ಈ ಎಲೆಕ್ಟ್ರೋ-ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫೀಲ್ಡ್‌ ಗೆ ಬೇಕಿದ್ದ ಗಣಿತವನ್ನು ಒದಗಿಸಿದವನು ಬೇರಾರೂ ಅಲ್ಲ, ನಾವೀಗಾಗಲೇ ಭೇಟಿ ನೀಡಿ ಬಂದಿರುವ ಜೇಮ್ಸ್ ಕ್ಲಾರ್ಕ್ ಮ್ಯಾಕ್ಸ್ವೆಲ್. ಮ್ಯಾಕ್ಸ್ವೆಲ್ ಒದಗಿಸಿದ ಈ ಗಣಿತದಿಂದಾಗಿ, ಈಗ “ಕ್ಲಾಸಿಕಲ್” ಎಂದು ಕರೆಯಿಸಿಕೊಳ್ಳುವ ಎಲೆಕ್ಟ್ರೋ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಥಿಯರಿ ಸಿದ್ಧವಾಯಿತು. ಮ್ಯಾಕ್ಸ್‌ವೆಲ್‌ ನ “ಆನ್ ಫ್ಯಾರಡೇಸ್ ಲೈನ್ಸ್ ಆಫ್ ಫೋರ್ಸ್” ವೈಜ್ಞಾನಿಕ ಲೇಖನ, ಗೆಲಿಲಿಯೋನ “ಇಲ್ ಸಜಿಯಟೋರೆ” ಪುಸ್ತಕದಂತೆಯೇ, ವಿಜ್ಞಾನದ ಇತಿಹಾಸದಲ್ಲಿಯೇ ಒಂದು ಮೈಲುಗಲ್ಲು. ಜೇಮ್ಸ್ ಮ್ಯಾಕ್ಸ್‌ವೆಲ್ ಕುರಿತು, ಐನ್‌ಸ್ಟೈನ್ “I owe more to Maxwell than to anyone” ಎಂದದ್ದು ಇದಕ್ಕಾಗಿಯೇ.

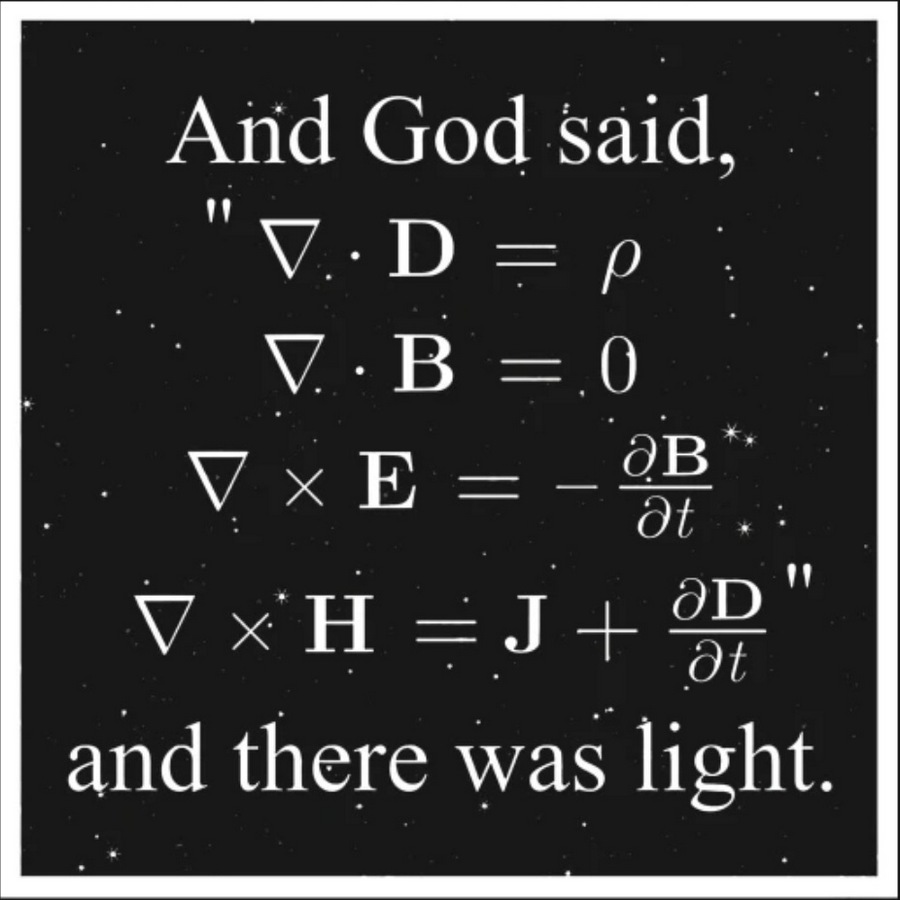
ವಿಜ್ಞಾನದ ಇತಿಹಾಸದಲ್ಲಿ ಹದಿನೇಳರಿಂದ ಹತ್ತೊಂಬತ್ತನೆಯ ಶತಮಾನದ ಕಾಲಘಟ್ಟ ಅತ್ಯಂತ ಮಹತ್ತರವಾದದು. ಈ ಕಾಲಘಟ್ಟದ ಆದಿಯಲ್ಲಿ, ಗೆಲಿಲಿಯೋ-ನ್ಯೂಟನ್ ಜೋಡಿ ಇದ್ದರೆ, ಅಂತ್ಯದಲ್ಲಿ ಫ್ಯಾರಡೆ-ಮ್ಯಾಕ್ಸ್ವೆಲ್ ಜೋಡಿ ಕಾಣುತ್ತಾರೆ. ಎರಡು ಶತಮಾನಗಳ ಅಂತರದ ಈ ಎರಡು ಜೋಡಿಗಳ ಕುರಿತು ಐನ್‌ಸ್ಟೈನ್ ಹೇಳುವ ಈ ಮಾತುಗಳನ್ನು ಗಮನಿಸಿ:

“… the pair Faraday-Maxwell has a most remarkable inner similarity with the pair Galileo-Newton – the former of each pair grasping the relations intuitively, and the second one formulating those relations exactly and applying them quantitatively”

*****

ಕಾಲ ಯಾರಿಗೂ, ಎಂದಿಗೂ ಬಗ್ಗುವುದಿಲ್ಲ ಎಂಬುದು ನಮ್ಮ ಅನುಭವ ಜನ್ಯ ವಿಚಾರ. ನಮ್ಮ ಪುರಾಣಗಳ ಚಿರಂಜೀವಿಗಳು ಕೂಡ, ಕಾಲವನ್ನು ಬಗ್ಗಿಸುವುದಿಲ್ಲ; ಕಾಲ ಅವರನ್ನು ಕೊಲ್ಲದೆ ಬಿಟ್ಟಿರಬಹುದು ಅಷ್ಟೇ. ಆದರೆ, ಅನಂತದ ಮಹಾ ಪುಸ್ತಕವನ್ನು, ಗೆಲಿಲಿಯೋನ ವಿಧಾನದಲ್ಲಿ ಓದಲು ತೊಡಗಿದರೆ, ಕಾಲ ಬಗ್ಗುವದಷ್ಟೇ ಅಲ್ಲ, ಕೃಷ್ಣ ರಂಧ್ರ ಗಳಂತಹ (Black Holes) ಆಕಾಶಕಾಯಗಳಲ್ಲಿ ಸೋತು ಸುಣ್ಣವಾಗಿ ಸತ್ತೇ ಬಿಡುತ್ತದೆ ಎಂಬುದು ಗೋಚರವಾಗುತ್ತದೆ.

ಕಾಲ ಸೋಲುವ ಈ ಸೋಜಿಗವನ್ನು ಅರ್ಥಮಾಡಿಕೊಳ್ಳಲು, ನಾವು ಮ್ಯಾಕ್ಸ್ವೆಲ್‌ ನ ಎಲೆಕ್ಟ್ರೋ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಥಿಯರಿಯ ಕಡೆಗೆ ಮತ್ತಷ್ಟು ಗಮನ ಹರಿಸಬೇಕು.

ಎಲೆಕ್ಟ್ರಿಸಿಟಿ ಮತ್ತು ಮ್ಯಾಗ್ನೆಟಿಸಂ ಒಂದನ್ನೊಂದು ಬಿಟ್ಟಿರುವುದಿಲ್ಲ. ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫೀಲ್ಡ್‌ ಗಳ ಗೆರೆಗಳನ್ನು, ಲೋಹದ ತಂತಿಯೊಂದರ ಮೂಲಕ ಕತ್ತರಿಸಿದರೆ, ಆ ತಂತಿಯಲ್ಲಿ ವಿದ್ಯುತ್ ಪ್ರವಾಹವಾಗುವುದನ್ನು ಫ್ಯಾರಡೆ ತೋರಿಸಿಕೊಟ್ಟ. ಮ್ಯಾಕ್ಸ್‌ವೆಲ್ ಇಂತಹ ವಿದ್ಯಮಾನಕ್ಕೆ ಬೇಕಿರುವ ಗಣಿತದ ಥಿಯರಿಯನ್ನು ಒದಗಿಸಿದ. ಈ ಥಿಯರಿಯ ಪ್ರಕಾರ, ಮ್ಯಾಗ್ನೆಟಿಕ್ ಅಥವಾ ಎಲೆಕ್ಟ್ರಿಕ್ ಫೀಲ್ಡ್‌ ಗಳನ್ನು ಕಲಕಿದಾಗ ಅಥವಾ ಕತ್ತರಿಸಿದಾಗ, ಶಾಂತವಾದ ಸರೋವರದೊಂದರಲ್ಲಿ ಕಲ್ಲೆಸೆದಾಗ ಮೂಡುವ ಅಲೆಗಳಂತೆ ಅಲೆಗಳು ಮೂಡುತ್ತವೆ. ಇವು ಎಲೆಕ್ಟ್ರೋ-ಮ್ಯಾಗ್ನೆಟಿಕ್ ಅಲೆಗಳು.

ಕಲ್ಲು ಬಿದ್ದ ಸ್ಥಳದಿಂದ, ಸರೋವರದ ಉದ್ದಗಲಕ್ಕೂ ನೀರಿನ ಅಲೆಗಳು ಸಂಚರಿಸುವಂತೆ, ಈ ಎಲೆಕ್ಟ್ರೋ-ಮ್ಯಾಗ್ನೆಟಿಕ್ ಅಲೆಗಳೂ ಸಹ ಅನಂತದ ವಿಶಾಲದಲ್ಲಿ ಸಂಚರಿಸುತ್ತವೆ. ಕಲ್ಲೆಸೆತದ ಕೇಂದ್ರದಿಂದ, ದೂರ ಸರಿದಂತೆ ನೀರಿನ ಅಲೆಗಳ ಎತ್ತರ ಕಡಿಮೆ ಆಗುವಂತೆ, ಈ ಎಲೆಕ್ಟ್ರೋ-ಮ್ಯಾಗ್ನೆಟಿಕ್ ಅಲೆಗಳ ಎತ್ತರವೂ ಕಡಿಮೆಯಾಗುತ್ತದೆ.

ಈ ಎಲೆಕ್ಟ್ರೋ-ಮ್ಯಾಗ್ನೆಟಿಕ್ ಅಲೆಗಳ ಸಂಚಾರದ ವೇಗ ಎಷ್ಟಿರಬಹುದು? ತನ್ನ ಗಣಿತದ ಮೂಲಕ ಇದನ್ನು ಲೆಕ್ಕ ಹಾಕಿದ ಮ್ಯಾಕ್ಸ್‌ವೆಲ್‌ ಗೆ ಆಶ್ಚರ್ಯವೊಂದು ಕಾದಿತ್ತು. ಅದರ ವೇಗ ಸೆಕೆಂಡಿಗೆ ಸುಮಾರು 300,000 ಕಿ.ಮೀ.ಗಳಷ್ಟು! ಅಂದರೆ, ಬೆಳಕಿನ ವೇಗದಷ್ಟೇ!!

ಇದು ತಿಳಿದ ನಂತರ, ಬೆಳಕೂ ಸಹ ಎಲೆಕ್ಟ್ರೋ-ಮ್ಯಾಗ್ನೆಟಿಕ್ ಅಲೆಗಳೇ ಎಂದು ಊಹಿಸಲು ಮ್ಯಾಕ್ಸ್ವೆಲ್‌ ಗೆ ಹೆಚ್ಚು ಸಮಯ ಬೇಕಾಗಲಿಲ್ಲ.

ಗೆಲಿಲಿಯೋ ಹೇಳಿದಂತೆ, ಗಣಿತದ ಭಾಷೆ, ಅನಂತವೆಂಬ ಮಹಾನ್ ಪುಸ್ತಕದ “ಬೆಳಕಿನ ಅಧ್ಯಾಯ”ವನ್ನು ಅರ್ಥವಾಗಿಸಿತ್ತು. ಆದರೆ, ವಿಜ್ಞಾನದಲ್ಲಿ ಯಾವುದಕ್ಕೂ ಕೊನೆಯಿಲ್ಲ. ಎಲ್ಲ ಉತ್ತರಗಳೂ ಮತ್ತಷ್ಟು ಪ್ರಶ್ನೆಗಳಿಗೆ ವಸ್ತುಗಳೇ.

ನೀರಿನ ಅಲೆಗಳೇನೋ ನೀರಿನಲ್ಲಿ ಸಂಚರಿಸುತ್ತವೆ. ನೀರಿಲ್ಲದೆ, ನೀರಿನ ಅಲೆಗಳಿಲ್ಲ. ಶಬ್ದದ ಅಲೆಗಳು ಸಂಚರಿಸಲು ಗಾಳಿಯೋ ಮತ್ತೊಂದು ಮಾಧ್ಯಮವೋ ಬೇಕು. ಹಾಗಿದ್ದರೆ, ಕೋಟ್ಯಂತರ ಮೈಲು ಸಂಚರಿಸುವ ಬೆಳಕಿನಂತಹ ಎಲೆಕ್ಟ್ರೋ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಅಲೆಗಳು ಸಂಚರಿಸುವುದಾದರೂ ಯಾವ ಮಾಧ್ಯಮದಲ್ಲಿ?!

ವಿಜ್ಞಾನ, ಅದರಲ್ಲೂ ಭೌತ ಶಾಸ್ತ್ರ, ಗೆಲಿಲಿಯೋ-ನ್ಯೂಟನ್ ನಂತರದ ಶತಮಾನಗಳಲ್ಲಿ, ಗಣಿತದ ಕೈಹಿಡಿದೇ ನಡೆದಿದೆ. ಅವರೀರ್ವರ ನಂತರ ಬಂದ ದೆಕಾರ್ತ್, ಹಯ್ಗೆನ್ಸ್, ಲಪ್ಲಾಸ್, ಮುಂತಾದ ಮಹಾನ್ ವಿಜ್ಞಾನಿಗಳು, ಗಣಿತ ಶಾಸ್ತ್ರದಲ್ಲೂ ಹೆಸರು ಮಾಡಿರುವುದು ಕೇವಲ ಕಾಕತಾಳೀಯವೇನಲ್ಲ.

ಇಡೀ ಜಗವನ್ನೇ ತೋಯಿಸಿ, ನಮ್ಮ ಜ್ಞಾನದ ಬಾಗಿಲನ್ನು ತೆರೆಯುವ, ರತ್ನದ ರಸವೂ – ಮುತ್ತಿನ ನೀರೂ ಆಗಿರುವ “ಬೆಳಕು” ಎಂದರೆ ಏನು? ಅದು ಯಾವುದರಿಂದ ಮಾಡಲ್ಪಟ್ಟಿದೆ? ಅದು ಹರಿಯುವ ವೇಗವೆಷ್ಟು? ಇಂತಹ ಪ್ರಶ್ನೆಗಳು ಸಹಸ್ರಾರು ವರ್ಷಗಳಿಂದ ಮನುಷ್ಯರನ್ನು ಕಾಡಿವೆ. ಅರೆ ತೆರೆದ ಕಿಟಕಿಯಿಂದ ಮನೆಯೊಳಗಿಳಿಯುವ ಬೆಳಕಿನ ಕೋಲು ಯಾರ ಮನದೊಳಗಿಳಿಯದು?!

ಶತಮಾನಗಳಿಂದ ಬೆಳಕಿನ ಮೇಲಿನ ಪರದೆಯನ್ನು ಸರಿಸುವ ಯತ್ನಗಳು ನಡೆಯುತ್ತಲೇ ಇವೆ. ಪುರಾತನ ಗ್ರೀಕ್ ತತ್ವಜ್ಞಾನಿ ಎಂಪೆಡೊಕ್ಲೆಸ್ ಎರಡೂವರೆ ಸಾವಿರ ವರ್ಷಗಳ ಹಿಂದೆಯೇ, ಬೆಳಕಿಗೊಂದು ವೇಗ ಇರಲೇಬೇಕೆಂದೆನ್ನುತ್ತಾನೆ. ಅವನ ದೃಷ್ಟಿಯಲ್ಲಿ, ಸೂರ್ಯನ ಬೆಳಕು ಭುವಿಯನ್ನು ತಲುಪಲು ಕೊಂಚವಾದರೂ ಸಮಯ ತೆಗೆದುಕೊಳ್ಳಲೇ ಬೇಕು. ಅವನ ನಂತರ ಬಂದ ಅರಿಸ್ಟಾಟಲ್, ಎಂಪೆಡೊಕ್ಲೆಸ್‌ ನನ್ನು ಉಲ್ಲೇಖಿಸುತ್ತಾನಾದರೂ, ಅವನ ವಾದವನ್ನು ಒಪ್ಪಿಕೊಳ್ಳಲು ಅಲ್ಲ; ಅರಿಸ್ಟಾಟಲ್‌ ನ ಪ್ರಕಾರ, ಬೆಳಕಿಗೊಂದು ವಸ್ತುವಿರಬಹುದಾದರೂ, ಅದಕ್ಕೆ ಚಲನೆ ಇಲ್ಲ; ಅದು ತತ್-ಕ್ಷಣವೇ ಚಲಿಸುವಂತಹದು. ಅರಿಸ್ಟಾಟಲ್ ನ ನಂತರ ಬಂದ ಯೂಕ್ಲಿಡ್, ಟಾಲೆಮಿಯಂತಹ ಮಹಾನ್ ವಿದ್ವಾಂಸರು, ದೃಗ್ವಿಜ್ಞಾನದ (Optics) ಕುರಿತು ಮಹತ್ವದ ವಿಚಾರಗಳನ್ನು ಚರ್ಚಿಸಿದ್ದಾರೆ. ಅವರ ದೃಷ್ಟಿಯಲ್ಲಿ, ಎಂಪೆಡೊಕ್ಲೆಸ್‌ ನ ವಾದವೇ ಸರಿ. ಆದರೆ, ಅವರ ಪ್ರಕಾರ, ಬೆಳಕು ಚಲಿಸುವುದು ಸೂರ್ಯ, ಚಂದ್ರ, ಬೆಂಕಿ ಇತ್ಯಾದಿಗಳಿಂದಲ್ಲ, ಬದಲಿಗೆ, ನಮ್ಮ ಕಣ್ಗಳಿಂದ! ಅವರ ನಂತರ ಬಂದ (ಇಂದಿನ ಈಜಿಪ್ಟಿನ) ಅಲೆಕ್ಸಾಂಡ್ರಿಯಾದ ಗಣಿತಜ್ಞ ಹೆರಾನ್, ಯೂಕ್ಲಿಡ್, ಟಾಲೆಮಿಯವರ “ಬೆಳಕಿರುವುದು ನಮ್ಮ ಕಣ್ಗಳಲ್ಲೇ” ಎಂಬ ವಾದವನ್ನು ಒಪ್ಪುತ್ತಾನಾದರೂ, ಅವನ ಪ್ರಕಾರ, ಅರಿಸ್ಟಾಟಲನೇ ಸರಿ. ನಾವು ಕಣ್ತೆರೆದ ತಕ್ಷಣವೇ ಕೋಟ್ಯಾಂತರ ಮೈಲು ದೂರದ ನಕ್ಷತ್ರಗಳನ್ನು ಕಾಣಬಹುದೆಂದರೆ, ಬೆಳಕಿಗೆ ಚಲನೆ ಇರುವುದು ಸಾಧ್ಯವಿಲ್ಲ (ಎಂದರೆ ಅದರ ವೇಗ ತತ್-ಕ್ಷಣದ್ದು), ಎನ್ನುತ್ತಾನೆ ಅವನು.

ಯೂಕ್ಲಿಡ್‌ ನ ಸಾವಿರ ವರ್ಷಗಳ ನಂತರ, ಹನ್ನೊಂದನೆಯ ಶತಮಾನದಲ್ಲಿ ಬಂದ ಅರೇಬಿಯನ್ ಮಹಾ ಗಣಿತಜ್ಞ ಹಸನ್ ಇಬ್ನ್ ಅಲ್-ಹತಮ್ (“ಅಲ್‌ಹೇಜ಼ೆನ್”) ಆಧುನಿಕ ದೃಗ್ವಿಜ್ಞಾನದ ಪಿತಾಮಹನೆಂದೇ ಹೆಸರಾದವನು. ಸೂರ್ಯ, ಚಂದ್ರರ ಗಾತ್ರ ದಿಗಂತದಿಂದ ಮೇಲೆ ಸರಿದಂತೆ ಕುಂದುವುದನ್ನು ವಿಶ್ಲೇಷಿಸುವ ಅಲ್‌ಹೇಜ಼ೆನ್, “ಕಿತಾಬ್ ಅಲ್-ಮನಜ಼ೀರ್” ಎಂಬ ದೃಗ್ವಿಜ್ಞಾನದ ಮಹಾ ಪುಸ್ತಕವನ್ನೇ ಬರೆದಿದ್ದಾನೆ. ಅವನ ಪ್ರಕಾರವೂ ಬೆಳಕಿಗೊಂದು ವೇಗವಿರಲೇಬೇಕು. ಅವನ ನಂತರ, ಹದಿಮೂರನೆಯ ಶತಮಾನದ ಪೋಲಿಷ್-ಜರ್ಮನ್ ವಿದ್ವಾಂಸ ವಿಟೆಲೋ, ಬೆಳಕು ಶೂನ್ಯದಲ್ಲಿ ಮಾತ್ರ ತತ್-ಕ್ಷಣದಲ್ಲಿ ಚಲಿಸುತ್ತದೆ ಎನ್ನುತ್ತಾನೆ. ಅವನ ಪ್ರಕಾರ, ಗಾಳಿ, ಗಾಜು, ನೀರಿನಂತಹ ವಸ್ತುಗಳು ಬೆಳಕಿನ ವೇಗವನ್ನು ಕಡಿಮೆ ಮಾಡುತ್ತವೆ.

ಹದಿನೇಳನೆಯ ಶತಮಾನದ ಹೊತ್ತಿಗೆ, ಯೂರೋಪಿಯನ್ ವಿಜ್ಞಾನಿಗಳಾದ ಕೆಪ್ಲರ್ ಮತ್ತು ದೆಕಾರ್ತ್, ಅರಿಸ್ಟಾಟಲನೇ ಸರಿ ಇರಬೇಕೆಂದೆನ್ನುತ್ತಾರೆ. ಅವರ ಪ್ರಕಾರ ಬೆಳಕಿನ ವೇಗ ತತ್-ಕ್ಷಣದ್ದು.

ಬೆಳಕಿನ ವೇಗವನ್ನು ಪ್ರಯೋಗಗಳ ಮೂಲಕ ಅರಿತುಕೊಳ್ಳಲು ಮೊದಲ ಬಾರಿಗೆ ಯತ್ನಿಸಿದವನು ಡಚ್ ವಿಜ್ಞಾನಿ ಐಸಾಕ್ ಬೀಕ್‌ಮನ್. ಗನ್ ಪೌಡರ್ ಅನ್ನು ಸ್ಫೋಟಿಸಿ, ಅದರ ಬೆಳಕನ್ನು ದೂರ-ದೂರದ ಕನ್ನಡಿಗಳಿಂದ ವೀಕ್ಷಿಸಿ, ಆ ಸಮಯವನ್ನು ಲೆಕ್ಕ ಹಾಕಿ ಅದರಿಂದ ವೇಗವನ್ನು ಅಳೆಯುವ ಯತ್ನ ಸಫಲವಾಗುವುದಿಲ್ಲ.

ಹದಿನೇಳನೆಯ ಶತಮಾನದ ಆರಂಭದ ಹೊತ್ತಿಗೆ, ಆಧುನಿಕ ಭೌತ ಶಾಸ್ತ್ರದ ಪಿತಾಮಹನೆನಿಸಿದ ಗೆಲಿಲಿಯೋನ ರಂಗ ಪ್ರವೇಶವಾಗುತ್ತದೆ. ಸ್ಪೋಟಕಗಳು ಸಿಡಿದಾಗ, ಅದರ ಬೆಳಕು ಅದರ ಸದ್ದಿಗೆ ಮೊದಲೇ ನಮ್ಮನ್ನು ತಲುಪುವುದನ್ನು ಗಮನಿಸುವ ಗೆಲಿಲಿಯೋ, ಬೆಳಕಿನ ವೇಗ ಶಬ್ದದ ವೇಗಕ್ಕಿಂತ ಎಷ್ಟೋ ಪಟ್ಟು ಹೆಚ್ಚಿರಬಹುದೆಂದು ಸರಿಯಾಗಿಯೇ ಊಹಿಸುತ್ತಾನೆ. ಬೆಳಕಿನ ವೇಗವನ್ನು ಅಳೆಯಲು ಗನ್ ಪೌಡರ್ ಬಳಸದ ಸರಳವಾದ ಪ್ರಯೋಗವೊಂದನ್ನು ಅವನು ಸೂಚಿಸುತ್ತಾನೆ.

ಗೆಲಿಲಿಯೋನ ಈ ಪ್ರಯೋಗಕ್ಕೆ ಎರಡು ಲಾಂದ್ರಗಳು ಮತ್ತು ಈರ್ವರು ವ್ಯಕ್ತಿಗಳು ಬೇಕು. ಪ್ರಯೋಗದ ಆದಿಯಲ್ಲಿ, ಈ ಇಬ್ಬರು ವ್ಯಕ್ತಿಗಳು ದೂರ-ದೂರದ ಎರಡು ದಿಬ್ಬಗಳ ಮೇಲೆ ನಿಲ್ಲಬೇಕು. ಮತ್ತು ಅವರ ಲಾಂದ್ರಗಳ ಬೆಳಕು ಕಾಣದಂತೆ ಅವುಗಳಿಗೊಂದು ಬಾಗಿಲಿರಬೇಕು. ಇಬ್ಬರೂ ದಿಬ್ಬ ಏರಿದ ಮೇಲೆ, ಮೊದಲನೆಯ ವ್ಯಕ್ತಿ ತನ್ನ ಲಾಂದ್ರದ ಬಾಗಿಲು ತೆರೆಯಬೇಕು. ಬಾಗಿಲು ತೆರೆದ ಸಮಯವನ್ನು ಮೊದಲನೆಯ ವ್ಯಕ್ತಿ (ತನ್ನ ಮನದಲ್ಲೇ) ದಾಖಲಿಸಿಕೊಳ್ಳಬೇಕು. ಅದು ಕಂಡ ತಕ್ಷಣವೇ, ಎರಡನೆಯ ವ್ಯಕ್ತಿ ತನ್ನ ಲಾಂದ್ರದ ಬಾಗಿಲನ್ನು ತೆರೆಯ ಬೇಕು. ಎರಡನೆಯ ವ್ಯಕ್ತಿಯ ಲಾಂದ್ರದ ಬೆಳಕು ಮೊದಲನೆಯ ವ್ಯಕ್ತಿಗೆ ಕಂಡ ಕೂಡಲೇ, ಆ ಸಮಯವನ್ನೂ ಅವನು ದಾಖಲಿಸಿಕೊಳ್ಳಬೇಕು. ದಿಬ್ಬದ ನಡುವಿನ ದೂರವನ್ನು ಅಳೆದರೆ, ಬೆಳಕಿನ ವೇಗ ಲೆಕ್ಕ ಹಾಕಲು ಸಾಧ್ಯವೆಂದು ಗೆಲಿಲಿಯೋನ ಅಂಬೋಣ.

ಆದರೆ, ಗಡಿಯಾರಗಳೇ ಇಲ್ಲದ ಆ ಕಾಲದಲ್ಲಿ, ಸಮಯವನ್ನು ದಾಖಲಿಸುವುದಾದರೂ ಹೇಗೆ? ಗೆಲಿಲಿಯೋ ಅದಕ್ಕೆ ಒದಗಿಸುವ ಪರಿಹಾರ: ನಮ್ಮ ಹೃದಯದ ಬಡಿತವನ್ನು ಗಡಿಯಾರದಂತೆ ಬಳಸುವುದು. ಗೆಲಿಲಿಯೋ, ಈ ವಿಧಾನವನ್ನು ಸೂಚಿಸುತ್ತಾನಾದರೂ, ಬೆಳಕಿನ ವೇಗವನ್ನು ಅಳೆಯುವ ಈ ಪ್ರಯೋಗ ಯಶಸ್ವಿಯಾಗಲಿಲ್ಲವೆಂದೂ ಹೇಳುತ್ತಾನೆ. ಅವನ ಮಾತು ಸತ್ಯವೂ ಸಹ. ಗೆಲಿಲಿಯೋ ಮತ್ತವನ ಸಹಾಯಕ, ಒಂದು ಮೈಲು ಅಂತರವಿರುವ ದಿಬ್ಬಗಳ ಮೇಲೆ ನಿಂತು ಪ್ರಯೋಗ ನಡೆಸಿದರೆ, ಬೆಳಕು ಆ ದೂರವನ್ನು ಕೇವಲ ೦.೦೦೦೦೦೫ ಸೆಕೆಂಡುಗಳಲ್ಲಿ ಸಂಚರಿಸುತ್ತದೆ. ಗೆಲಿಲಿಯೋನ ಹೃದಯದ ಬಡಿತ ನಿಮಿಷಕ್ಕೆ ೧.೨ ಕೋಟಿ ಇದ್ದಿದ್ದಲ್ಲಿ, ಬೆಳಕಿನ ವೇಗವನ್ನು ಅಳೆಯಲು ಸಾಧ್ಯವಿತ್ತೇನೋ!!

*****

ಬೆಳಕಿನ ವೇಗವನ್ನು ಅಳೆಯಲು ನಮಗೆ ಮೊದಲು ಯಶ ದೊರಕಿದ್ದು ಚಂದ್ರನ ಸಹಾಯದಿಂದ. ಆದರೆ, ಆ ಚಂದ್ರ, ನಮ್ಮ ಚಂದ್ರನಲ್ಲ. ಗುರುಗ್ರಹದ ಚಂದ್ರ. ಗುರುವಿಗೆ ಒಬ್ಬ ಚಂದ್ರನಲ್ಲ, ೭೯ ಚಂದ್ರಗಳಿವೆ. ಅದರಲ್ಲಿ “ಇಯೋ” ಎನ್ನುವುದೂ ಒಂದು. (ಗ್ರೀಕ್ ಪುರಾಣಗಳ ಪ್ರಕಾರ, “ಇಯೋ”, ದೇವತೆಗಳ ರಾಜ ಜ್ಯೂಪಿಟರ್‌ ನ ಪ್ರೇಯಸಿ. ಹೀಗಾಗಿ, “ಇಯೋ”ವನ್ನು ಚಂದ್ರನೆನ್ನುವ ಬದಲು “ಚಂದ್ರಿಕೆ” ಎನ್ನುವದೇ ಸೂಕ್ತವಿರಬಹುದೇ…!)

ಗೆಲಿಲಿಯೋನ “ಪ್ರಯೋಗ”ಗಳ ಸುಮಾರು ಐವತ್ತು ವರ್ಷಗಳ ನಂತರ. ಡೆನ್ಮಾರ್ಕಿನ ಭೌತಶಾಸ್ತ್ರಜ್ಞ ರೋಮರ್, ಕ್ರಿ.ಶ.೧೬೭೬ರಲ್ಲಿ “ಇಯೋ”ಳ ಚಲನವಲನಗಳನ್ನು ಅತ್ಯಂತ ಕ್ರಮಬದ್ಧವಾಗಿ ವೀಕ್ಷಿಸುತ್ತಿದ್ದ. ನಮ್ಮ “ಚಂದ್ರ ಗ್ರಹಣ”ದಂತೆ, ಈ “ಇಯೋ”ಳ ಗ್ರಹಣವೂ ಆಗ್ಗಿಂದಾಗ್ಗೆ ಆಗುತ್ತಲೇ ಇರುತ್ತದೆ. ಈ ಗ್ರಹಣಗಳನ್ನು ಗಮನಿಸುತ್ತಿದ್ದಾಗ, ಅವನಿಗೊಂದು ಸಂಗತಿ ಗಮನಕ್ಕೆ ಬಂತು. ಕೆಲವೊಮ್ಮೆ ಗ್ರಹಣ ಗೋಚರವಾಗುವುದು ಲೆಕ್ಕಾಚಾರಕ್ಕಿಂತ ಸುಮಾರು ಎಂಟು-ಹತ್ತು ನಿಮಿಷ ನಿಧಾನವಾಗುತ್ತಿತ್ತು. ಅದರ ಬಗೆಗೆ, ಅವನು ಮತ್ತಷ್ಟು ಅಧ್ಯಯನ ನಡೆಸಿದಾಗ, ಅವನಿಗೆ ಒಂದು ವಿಷಯದ ಅರಿವಾಯಿತು. ಗುರು ಮತ್ತು ಭೂಮಿಗಳು ಸೂರ್ಯನ ಸುತ್ತ ಸುತ್ತುವಾಗ, ಅವುಗಳ ನಡುವಿನ ಅಂತರ ಬದಲಾಗುತ್ತಿರುತ್ತದೆ. ಗುರು ಮತ್ತು ಭೂಮಿಗಳ ಅಂತರ ಹೆಚ್ಚಿದ್ದಾಗ, ಇಯೋ-ಗ್ರಹಣ ನಿಧಾನವಾಗಿ ಗೋಚರಿಸುವುದನ್ನು ಅವನು ಕಂಡುಕೊಂಡ. ಮತ್ತು ಅದರ ಕಾರಣವನ್ನು ಅವನು ಸರಿಯಾಗಿಯೇ ಊಹಿಸಿದ: ಇಯೋಳಿಂದ ಪ್ರತಿಫಲಿಸುವ ಸೂರ್ಯನ ಬೆಳಕು ಆ ಹೆಚ್ಚುವರಿ ದೂರವನ್ನು ಕ್ರಮಿಸಬೇಕಿತ್ತು!

ಈ ವಿಷಯದ ಕುರಿತು ಮತ್ತಷ್ಟು ಅಧ್ಯಯನ ನಡೆಸಿದ ರೋಮರ್, ಇಯೋಳಿಂದ ಪ್ರತಿಫಲಿತವಾಗುವ ಬೆಳಕು ಭೂಮಿಯನ್ನು ತಲುಪಲು ಸುಮಾರು ೨೨ ನಿಮಿಷಗಳು ಬೇಕೆಂದು ಅವನು ಒಂದು ಅಂದಾಜು ಮಾಡಿದ.

ಕೆಲ ವರ್ಷಗಳ ನಂತರ ರೋಮರ್‌ ನ ಇಯೋ-ಅಧ್ಯಯನದ ವಿವರಗಳು ನ್ಯೂಟನ್‌ ನನ್ನು ಮುಟ್ಟಿದವು. ಎಲ್ಲವನ್ನು ಖಚಿತತೆಯಿಂದ ಲೆಕ್ಕಹಾಕುವ ನ್ಯೂಟನ್, ಮತ್ತಷ್ಟು ಲೆಕ್ಕಾಚಾರ ಮಾಡಿ, ತನ್ನ ಪ್ರಿಂಕಿಪಿಯಾದಲ್ಲಿ ಒಂದು ತೀರ್ಮಾನಕ್ಕೆ ಬಂದ: “ಸೂರ್ಯನ ಬೆಳಕು ಭೂಮಿಯನ್ನು ಮುಟ್ಟಲು ಸುಮಾರು ಏಳರಿಂದ ಎಂಟು ನಿಮಿಷಗಳು ಬೇಕು”

ನ್ಯೂಟನ್‌ ನ ಈ ಲೆಕ್ಕ, ನಮ್ಮ ಇತ್ತೀಚಿನ ಅಂದಾಜಿಗಿಂತ ತೀರಾ ದೂರವೇನಿಲ್ಲ. ವರ್ಷದುದ್ದಕ್ಕೂ ಸೂರ್ಯ-ಭೂಮಿಯರ ನಡುವಿನ ಅಂತರ ಹೆಚ್ಚು-ಕಡಿಮೆ ಆಗುತ್ತಲೇ ಇರುತ್ತದೆ. ಹೀಗಾಗಿ, ಸೂರ್ಯನ ಬೆಳಕು ಭುವಿಯನ್ನು ಮುಟ್ಟುವ ಸಮಯವೂ ಬದಲಾಗುತ್ತಲೇ ಇರುತ್ತದೆ. ಆದರೆ, ಈ ಸಮಯವನ್ನು ಸರಾಸರಿಯಾಗಿ ಹೇಳುವುದಾದರೆ, ಸುಮಾರು ಎಂಟು ನಿಮಿಷ ೨೦ ಸೆಕೆಂಡುಗಳು ಎನ್ನಬಹುದು.

ಸೂರ್ಯನಿಂದ ಭೂಮಿಗೆ ಬೆಳಕಿನ ಪ್ರಯಾಣದ ಸಮಯವನ್ನೇನೋ ಕಂಡುಕೊಂಡಿದ್ದಾಯಿತು. ಆದರೆ, ವೇಗವನ್ನು ಅಳೆಯಲು, ಸೂರ್ಯ-ಭೂಮಿಯ ನಡುವಿನ ಅಂತರವೂ ಬೇಕಲ್ಲ! (ಸೂರ್ಯನ ದೂರವನ್ನು ತಿಳಿಯಲು ಹನ್ನೊಂದು ವರ್ಷಗಳ ಕಾಲ ಪರ್ಯಟನೆ ಮಾಡಿದ ಲೆ ಜ಼ೆಂಟಿಯ ಕಥಾನಕವನ್ನು ಇಲ್ಲಿ ಓದಿರಿ: https://bit.ly/3bgYRi2

ನಾವು ಹೈ-ಸ್ಕೂಲಿನಲ್ಲಿ ಕಲಿಯುವ ಟ್ರಿಗನಾಮೆಟ್ರಿ ಮತ್ತು ಪ್ಯಾರಲಾಕ್ಸ್ ವಿಧಾನದ ಸಹಾಯದಿಂದ ಆಕಾಶಕಾಯಗಳ ನಡುವಿನ ಅಂತರವನ್ನು ಲೆಕ್ಕ ಹಾಕಬಹುದು. ಹದಿನೇಳನೆಯ ಶತಮಾನದ ವೇಳೆಗೆ ಈ ವಿಧಾನದ ಪ್ರಕಾರ, ಭೂಮಿ ಮತ್ತು ಸೂರ್ಯನ ನಡುವಿನ ಅಂತರ ಸುಮಾರು ೪೦ ರಿಂದ ೯೦ ದಶ ಲಕ್ಷ ಮೈಲುಗಳಿರಬಹುದೆಂದು ವಿಜ್ಞಾನಿಗಳು ಊಹಿಸಿದ್ದರು.

ಕ್ರಿ.ಶ. ೧೬೭೮ರಲ್ಲಿ, ಪ್ರಪ್ರಥಮ ಬಾರಿಗೆ, ರೋಮರ್‌ ನ ಅಧ್ಯಯನವನ್ನು ಬಳಸಿ, ಡಚ್ ವಿಜ್ಞಾನಿ ಕ್ರಿಶ್ಚಿಯಾನ್ ಹಯ್ಗೆನ್ಸ್ ಬೆಳಕಿನ ವೇಗವನ್ನು ಲೆಕ್ಕ ಹಾಕಿದ. ಅವನ ಲೆಕ್ಕಾಚಾರದಂತೆ, ಅದರ ವೇಗ ಸೆಕೆಂಡಿಗೆ ಸುಮಾರು ೨೩೪,೦೦೦ ಕಿ.ಮೀ.ಗಳು. ಹಯ್ಗೆನ್ಸ್‌ ನ ಲೆಕ್ಕಾಚಾರವನ್ನು ಮತ್ತಷ್ಟು ಸುಧಾರಣೆ ಮಾಡಿ, ೧೬೯೪ರಲ್ಲಿ ಇಂಗ್ಲೀಷ್ ವಿಜ್ಞಾನಿ ಎಡ್ಮಂಡ್ ಹೇಲಿ ಬೆಳಕಿನ ವೇಗ ಸೆಕೆಂಡಿಗೆ ಸುಮಾರು ೩ ಲಕ್ಷ ಕಿ.ಮೀ.ಗಳೆಂದು ತೀರ್ಮಾನಕ್ಕೆ ಬಂದ. (ಇತ್ತೀಚಿನ ವಿಜ್ಞಾನಿಗಳ ಪ್ರಕಾರ ಈ ವೇಗ ಸೆಕೆಂಡಿಗೆ 299792.458 ಕಿ.ಮೀ.ಗಳು)

ಕೊನೆಗೂ ಬೆಳಕಿನ ರಹಸ್ಯವೊಂದು ಹೊರಬಿದ್ದಿತ್ತು. ಬೆಳಕಿಗೂ ಒಂದು ಚಲನವಿದೆ, ಆ ಚಲನೆಗೆ ನಿಶ್ಚಿತವಾದ ಒಂದು ವೇಗವೂ ಇದೆ ಎಂಬ ಸಂಗತಿ ಅರಿಸ್ಟಾಟಲ್‌ ನ ತತ್-ಕ್ಷಣದ ಬೆಳಕಿನ ವಾದವನ್ನು ಮೂಲೆಗೆ ತಳ್ಳಿತ್ತು. ಆದರೆ, ನ್ಯೂಟನ್, ಬೆಳಕಿನ ವೇಗವನ್ನು ನಿರ್ಧರಿಸಲು ಸಹಾಯ ಮಾಡುತ್ತಲೇ, ಬೆಳಕಿನ ಇನ್ನೊಂದು ಅಂಶದ ಕುರಿತು ವಾದವೊಂದರ ಹುಟ್ಟುಹಾಕಿದ್ದ.

*****

(ಮುಂದುವರೆಯುವುದು)